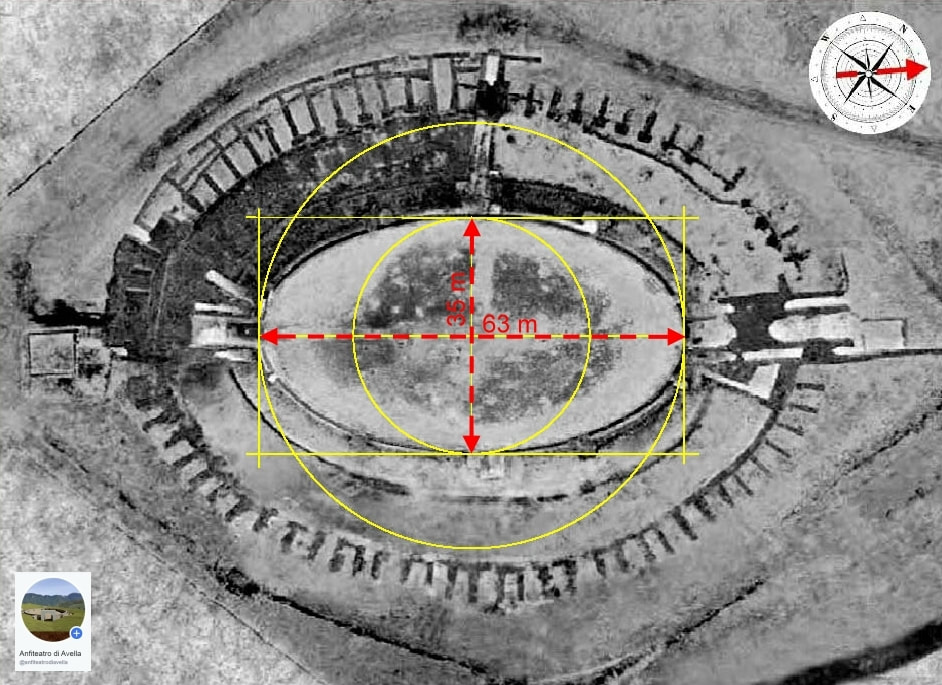
Dimensioni dell'arena, piede più piede meno.
Sono state determinate geometricamente tracciando le tangenti nei 4 punti estremi della curva dell'arena.
Seguirà aggiornamento.
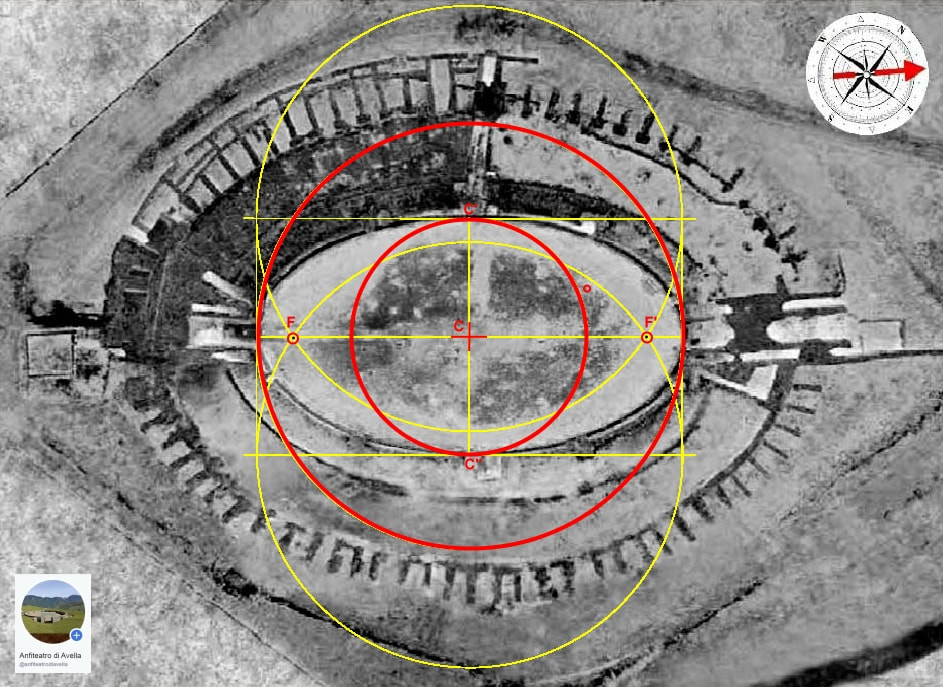
Centro e fuochi.
Volendoli anche misurare possiamo dedurre che essi sono a una distanza di 28,22m dal centro C.
La funzione dei fuochi.
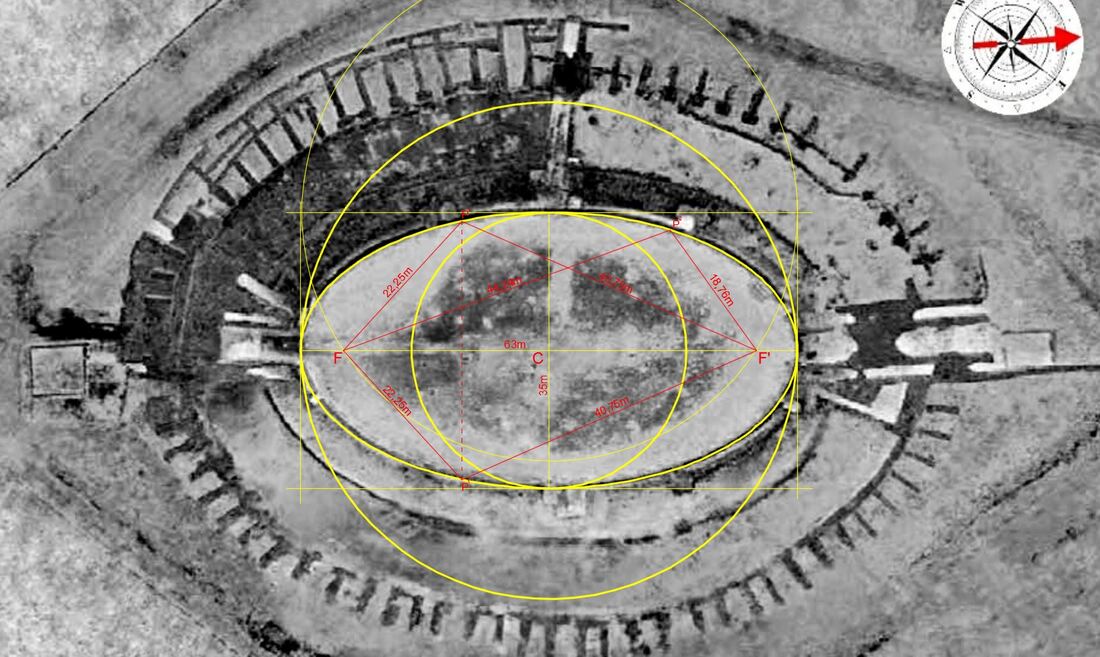
Una volta che abbiamo intercettati i fuochi F e F' lungo l'asse maggiore dell'arena del nostro anfiteatro, possiamo verificare come la somma della distanza di qualsiasi punto P, appartenente alla curva di delimitazione dell'arena, rispetto a F e F' sia la stessa per ognuno di essi e che essa sia proprio pari alla lunghezza dell'asse maggiore, cioè nel nostro caso 63m.
Infatti nell'immagine riprodotta, che rappresenta in scala l'anfiteatro di Avella con la sua arena, possiamo verificare come per esempio il punto P1 sia distante dal fuoco F 22,25m e dal fuoco F' 40,75m e che la somma di queste distanze sia proprio 63m. Lo stesso dicasi per il punto P2 la cui distanza da F è 44,24 e da F' 18,76m, la cui somma è anch'essa 63m. Come si può anche facilmente verificare che le distanze dei punti P', simmetrici rispetto all'asse maggiore siano proprio le stesse dei punti P.
Proseguendo così, quindi, per ogni punto della curva che circoscrive l'arena, possiamo verificare che tutti rispondono a questa regola che definisce un curva ovale perfetta come ellisse.
L'arena ellittica dell'anfiteatro avellano. Oltre la matematica c'è la geometria a dimostrarla.
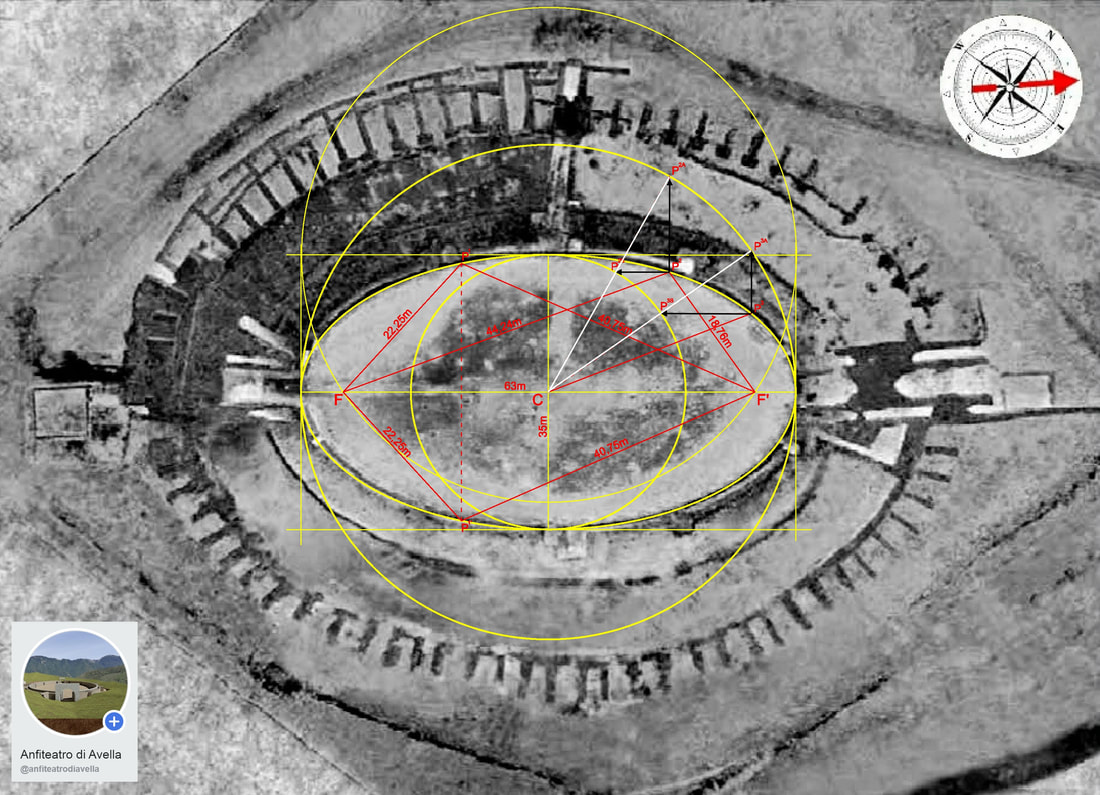
Utilizziamo lo stesso schema, con il quale abbiamo dimostrato la forma ellittica dell’arena, visto che preso ogni punto P del bordo dell'arena la somma della sua distanza dai due fuochi dà sempre lo stesso risultato 63m - lunghezza dell'asse maggiore – per dimostrarlo anche geometricamente.
Infatti, prendendo un punto P qualsiasi dell'estremo dell'arena, per esempio P2, e proiettandolo parallelamente all'asse verticale sul cerchio che circoscrive l'arena, otterremo il punto P2A. Lo stesso punto P2 lo proiettiamo parallelamente all'asse orizzontale sul cerchio inscritto all'arena, ottenendo il punto P3A. Unendo anche i due punti P2A e P3A otteniamo un segmento che prolungato verso l'interno dell'arena incrocia proprio il punto C, che rappresenta il suo centro. Applicando lo stesso procedimento per tutti i punti estremi dell’arena, otterremo tutti segmenti che convergono verso il centro C. La dimostrazione questa che anche attraverso la costruzione geometrica, l'ellisse resta confermata come forma dell'arena.
A questo punto la domanda è: con quale metodo l'architetto dell'epoca, dopo averla pensata così perfetta, sia riuscito a realizzarla altrettanto perfettamente suol luogo prescelto?


 Feed RSS
Feed RSS
